Research

I am a mathematician in the Department of Mathematics at the University of Manchester.  By day I research extremal combinatorics, and by night I talk maths at anyone who will listen.

I have an annotated bibliography of my papers, and an open notebook of things I’ve learnt and don’t want to forget.

email: first.last@manchester.ac.uk

Research interests

Extremal combinatorics

Understanding large discrete objects is both increasingly important in practice and computationally difficult. Extremal combinatorics seeks to answer questions of the form “how large/small can a discrete structure be so that a given property does/does not hold?” By probing the extreme cases of difficult problems we can learn about their structure, for example by discovering simpler necessary or sufficient conditions for properties to hold.

Ramsey theory

In any group of six people, either some three people all know each other or there are some three people none of whom know either of the others. This is the beginning of Ramsey theory, the study of unavoidable patterns in large unstructured objects. The patterns I look for are infinite, and the tools used to find them are surprising; many results rely on “ultrafilters”, objects which are known to exist but are impossible to specify precisely.

Publications

All of my papers are available from the arXiv or in a variety of formats from the individual blog posts linked below.

  1. Small sums of five roots of unity
  2. Isoperimetric stability in lattices (with Joshua Erde, Peter Keevash and Alexander Roberts).
  3. The Namer-Claimer game. Discrete Mathematics, Volume 344, Issue 3, March 2021, 112256.
  4. Minimalist designs (with Stefan Glock, Daniela Kühn, Allan Lo, Richard Montgomery and Deryk Osthus). Random Struct Alg. 2020; 57: 47– 63.
  5. Isoperimetry in integer lattices (with Joshua Erde). Discrete Analysis 2018:7, 16pp.
  6. Clique decompositions of multipartite graphs and completion of Latin squares (with Daniela Kühn, Allan Lo, Deryk Osthus and Amelia Taylor). J. Combin. Theory Ser. A 151 (2017), 146–201.
  7. Fractional clique decompositions of dense graphs and hypergraphs (with Daniela Kühn, Allan Lo, Richard Montgomery and Deryk Osthus). J. Combin. Theory Ser. B 127 (2017), 148–186.
  8. Edge-decompositions of graphs with high minimum degree (with Daniela Kühn, Allan Lo and Deryk Osthus). Adv. Math. 288 (2016), 337–385.
  9. Distinguishing subgroups of the rationals by their Ramsey properties (with Neil Hindman, Imre Leader and Dona Strauss). J. Combin. Theory Ser. A 129 (2015), 93–104.
  10. Partition regularity without the columns property (with Neil Hindman, Imre Leader and Dona Strauss). Proc. Amer. Math. Soc. 143 (2015), no. 8, 3387–3399.
  11. Partition regularity of a system of De and Hindman. INTEGERS 14 (2014), #A31, 7pp.
  12. Maximum hitting for 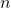n sufficiently large. Graphs Combin. 30 (2014), no. 2, 267–274.
  13. Random walks on quasirandom graphs (with Eoin Long). Electron. J. Combin. 20 (2013), no. 4, Paper 25, 18 pp.
  14. Partition regularity with congruence conditions (with Imre Leader). J. Combin. 4 (2013), no. 3, 293–297.
  15. Partition regularity in the rationals (with Neil Hindman and Imre Leader). J. Combin. Theory Ser. A 120 (2013), no. 7, 1590–1599.
  16. A note on balanced independent sets in the cube. Australas. J. Combin. 52 (2012), 205–207.