- search.c
- 221000.dat
- plot5.ggb – Geogebra notebook
- geo5.sh – awk one-liner to format array to input parameters to Geogebra
Errata
Every time I wrote ![]() I should have written
I should have written ![]() . This will be corrected in the final version.
. This will be corrected in the final version.
The pigeonhole upper bound is perhaps better written ![]() , since it arises as
, since it arises as ![]() , where
, where ![]() is the totient function.
is the totient function.
Quality of the data
After commenting, Tomás Oliveira e Silva sent a follow-up email prompting me to belatedly flesh out this post a little.
After computing the first 100000 values independently, he found one discrepancy. 221000.dat has
53829 1.035945566231253e-8 6045 19754 30497 38849but Tomás has
53829 0.0000000043404367309945397 0 0 15622 31244 31244which agrees with the output of search.c
53829 4.3404373281240489e-09 0 15622 31244 31244So what’s going on here? The answer necessarily includes the fact that search.c was not used to produce that line of 221000.dat. The history is that the data set and the search program developed together over time. The final version of search.c is (hopefully) better than the earliest versions in several ways, including a considered approach to avoiding zero sums rather than an optimistic one, and a change in the enumeration order to notice when we’re about to generate a lot of very long sums and skip over them. The very earliest searches weren’t even done in C; I used Haskell, which is my usual go to for combinatorics, but wasn’t the best fit for this naturally expressed brute force loop. In any case, I didn’t rerun the whole search using the final program because of the cost of producing the data. I’ve been at peace with the risk of errors because I was using the data to suggest patterns to investigate rather than relying on it for any proofs, but I should have been clearer about what I did.
Putting my archaeologist’s hat on, we can tell that the line in 221000.dat isn’t from the latest version of search.c due to the different output format. In fact, there’s a break between the two formats at ![]() .
.
119999 1.6533522139157386e-9 15853 43211 70569 86422
120000 3.4249738497730593e-10 20224 40448 77495 82953
120001 8.4593861872462649e-10 10962 39803 71356 79549
120002 1.4113956883942480e-10 19401 45243 71085 90486
120003 1.3630084760844623e-10 10265 44351 65134 85917
120004 5.3309237833505616e-10 9345 39651 69957 79302
120005 2.1493219522622943e-09 6408 39397 67265 79033This means that I might have used Haskell as far as 120000 (I might also have used C with a different output format), but I didn’t use it any later. In fact the incorrect line matches the output of the Haskell search exactly, so the error probably comes from a bug in the Haskell. My first guess, given the correct form of the optimal configuration for 53829, is that I had an off by one error in an index preventing me from looking at ![]() , but after revisiting the source code I don’t think that’s it. As an early version of the guard against pointless searching I have the line
, but after revisiting the source code I don’t think that’s it. As an early version of the guard against pointless searching I have the line
bestCompletions bestGuess a b = if length > 2.0 then [] else [t | t@(_,a,b,c,d) <- candidates''', not $ zero a b c d]The error here is that the cutoff for “too long” needs to be 2 plus the shortest thing seen so far, not 2. (Not counting the triple-prime in a variable name as an error.) The correct configuration for 53829 is exactly a situation in which the sum of the triple has length just over 2, so the Haskell search couldn’t see it.
I’m going to generate the data from 1 to 120000 again in case there are more errors of this type.
Hello Ben,
By using the double data type you have to pay attention to round-off errors. specially when the non-zero sum is very small. For example, for n=90681, your smallest non-zero sum has only one or two significant digits; the rest is garbage. Maybe %18.16f would have been better than %.16e, as only one, maybe two wrong digits would have been displayed.
Anyway, I’m in the middle of checking your results up to n=100000. My own program is about 4 times slower than yours, but it uses twice the precision (libqd-dev in GNU/linux), so round-off errors will not be a problem even for larger n. For each (n,a,b) I always check 8 cases. It appears that by making c=(u-v)/2 and d=(u+v)/2 and by working with u and v instead of c and d, it is easier to find the best (c,d) combination. Indeed, in those coordinates the shape of the squared error surface is particularly simple (to second order, two decoupled variables and squared error = sum of two one-dimensional parabolas).
I’l get back to you in a few days when the computations are finished. It would be interesting to go up to 1 million, but the cubic nature on the whole effort is not our friend (10^ 5 in 2.5 days in my 8-core laptop, 10^6 in 2500 days…)
Best regards,
TOS
Yes, I should have paid closer attention to what I could achieve with doubles — I didn’t do much more than note that I’d have serious problems if the sums got below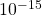 , and as you point out it does get pretty close. I’m more relaxed about the output precision as the goal was to be able to read the values back if necessary, rather than a claim that all of the digits were correct.
, and as you point out it does get pretty close. I’m more relaxed about the output precision as the goal was to be able to read the values back if necessary, rather than a claim that all of the digits were correct.
I’m pleased someone’s checking my numbers, and will respond to your follow up email in the original post.