The conventional statement of linear programming duality is completely inscrutable.
- Prime: maximise
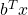 subject to
subject to 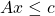 and
and 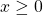 .
. - Dual: minimise
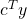 subject to
subject to 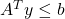 and
and 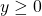 .
.
If either problem has a finite optimum then so does the other, and the optima agree.
I do understand concrete examples. Suppose we want to pack the maximum number vertex-disjoint copies of a graph ![]() into a graph
into a graph ![]() . In the fractional relaxation, we want to assign each copy of
. In the fractional relaxation, we want to assign each copy of ![]() a weight
a weight ![]() such that the weight of all the copies of
such that the weight of all the copies of ![]() at each vertex is at most
at each vertex is at most ![]() , and the total weight is as large as possible. Formally, we want to
, and the total weight is as large as possible. Formally, we want to
maximise ![]() subject to
subject to ![]() and
and ![]() ,
,
which dualises to
minimise ![]() subject to
subject to ![]() and
and ![]() .
.
That is, we want to weight vertices as cheaply as possible so that every copy of ![]() contains
contains ![]() (fractional) vertex.
(fractional) vertex.
To get from the prime to the dual, all we had to was change a max to a min, swap the variables indexed by ![]() for variables indexed by
for variables indexed by ![]() and flip one inequality. This is so easy that I never get it wrong when I’m writing on paper or a board! But I thought for years that I didn’t understand linear programming duality.
and flip one inequality. This is so easy that I never get it wrong when I’m writing on paper or a board! But I thought for years that I didn’t understand linear programming duality.
(There are some features of this problem that make things particularly easy: the vectors ![]() and
and ![]() in the conventional statement both have all their entries equal to
in the conventional statement both have all their entries equal to ![]() , and the matrix
, and the matrix ![]() is
is ![]() -valued. This is very often the case for problems coming from combinatorics. It also matters that I chose not to make explicit that the inequalities should hold for every
-valued. This is very often the case for problems coming from combinatorics. It also matters that I chose not to make explicit that the inequalities should hold for every ![]() (or
(or ![]() , as appropriate).)
, as appropriate).)
Returning to the general statement, I think I’d be happier with
- Prime: maximise
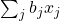 subject to
subject to 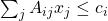 and
and 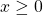 .
. - Dual: minimise
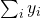 subject to
subject to 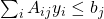 and
and 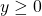 .
.
My real objection might be to matrix transposes and a tendency to use notation for matrix multiplication just because it’s there. In this setting a matrix is just a function that takes arguments of two different types (![]() and
and ![]() or, if you must,
or, if you must, ![]() and
and ![]() ), and I’d rather label the types explicitly than rely on an arbitrary convention.
), and I’d rather label the types explicitly than rely on an arbitrary convention.