A filter on ![]() is a consistent notion of largeness for subsets of
is a consistent notion of largeness for subsets of ![]() . “Largeness” has the following properties.
. “Largeness” has the following properties.
- if
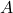 is large and
is large and 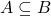 then
then 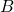 is large
is large - if
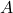 and
and 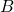 are large then
are large then  is large
is large - the empty set is not large
At most one of ![]() and
and ![]() is large; an ultrafilter is a filter which always has an opinion about which it is.
is large; an ultrafilter is a filter which always has an opinion about which it is.
- either
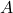 or
or 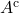 is large
is large
The usual notation for “![]() is large” is
is large” is ![]() , where
, where ![]() is the ultrafilter. This casts ultrafilters as sets, rather than notions of largeness. To bring the notion of largeness to the foreground we can use ultrafilter quantifiers; we write
is the ultrafilter. This casts ultrafilters as sets, rather than notions of largeness. To bring the notion of largeness to the foreground we can use ultrafilter quantifiers; we write ![]() , read “for
, read “for ![]() -most
-most ![]() ,
, ![]() holds” (where we have also identified
holds” (where we have also identified ![]() with the predicate “is a member of
with the predicate “is a member of ![]() “).
“).
- if
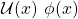 and
and  then
then 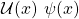
- if
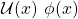 and
and 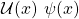 then
then 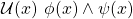
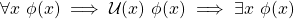
![Rendered by QuickLaTeX.com \neg [\U(x)\ \phi(x)] \iff \U(x)\ \neg \phi(x)](https://babarber.uk/wp-content/ql-cache/quicklatex.com-24f4c82b972af71f40dc8d9cb3222f71_l3.png)
From this point of view ![]() says that the set of elements with property
says that the set of elements with property ![]() is everything, and
is everything, and ![]() that the set of elements with property
that the set of elements with property ![]() is non-empty.
is non-empty. ![]() behaves like a mixture of
behaves like a mixture of ![]() and
and ![]() , with the considerable advantage that logical operations pass through
, with the considerable advantage that logical operations pass through ![]() unchanged without having to worry about De Morgan’s laws.
unchanged without having to worry about De Morgan’s laws.
Adding ultrafilters
It turns out that the set of ultrafilters on ![]() is a model for the Stone–Čech compactification
is a model for the Stone–Čech compactification ![]() of
of ![]() .
. ![]() is embedded as the set of principal ultrafilters (“
is embedded as the set of principal ultrafilters (“![]() is large if and only if
is large if and only if ![]() “), and the addition on
“), and the addition on ![]() extends to
extends to ![]() :
:
![]()
(Here ![]() should be interpreted as
should be interpreted as ![]() .) But to use this addition with quantifiers all we need to know is that
.) But to use this addition with quantifiers all we need to know is that ![]() . If you can see that from the first definition then your brain is wired differently from mine.
. If you can see that from the first definition then your brain is wired differently from mine.
It is a fact that there exist idempotent ultrafilters, with ![]() . Given such a
. Given such a ![]() , we can play the following game. Suppose that
, we can play the following game. Suppose that ![]() . Then
. Then ![]() , so
, so ![]() and therefore
and therefore ![]() (by ANDing with the original assertion, and the original assertion with the dummy variable
(by ANDing with the original assertion, and the original assertion with the dummy variable ![]() replaced by
replaced by ![]() ). In particular,
). In particular, ![]() . But now we can fix a good choice of
. But now we can fix a good choice of ![]() and repeat the whole process with
and repeat the whole process with ![]() in place of
in place of ![]() to get that
to get that
![]()
Iterating, we eventually obtain an infinite sequence ![]() such that
such that ![]() holds for every sum of finitely many of the
holds for every sum of finitely many of the ![]() . Together with the observation that whenever
. Together with the observation that whenever ![]() is finitely coloured exactly one of the colour classes is
is finitely coloured exactly one of the colour classes is ![]() -large this proves Hindman’s theorem, that we can always find an infinite sequence
-large this proves Hindman’s theorem, that we can always find an infinite sequence ![]() such that every sum of finitely many terms has the same colour.
such that every sum of finitely many terms has the same colour.
A version of this argument with more of the details filled in is on the Tricki.