Counting colourings with containers

On the maximum number of integer colourings with forbidden monochromatic sums, Hong Liu, Maryam Sharifzadeh and Katherine Staden

Maryam spoke about this paper at this week’s combinatorics seminar.

The problem is as follows. Let $f(A, r)$ be the number of $r$ -colourings of a subset $A$ of $[n]$ with no monochromatic sum $x + y = z$ . What is the maximum $f(n,r)$ of $f(A, r)$ over all $A \subseteq [n]$ ?

One possibility is that we take $A$ to be sum-free, so that $f(A, r) = r^{|A|}$ . The maximum size of a sum-free set of $[n]$ is around $n/2$ , achieved by the set $O$ of odd numbers and the interval $I = [\lfloor n/2 \rfloor + 1, n]$ , so $f(n, r) \geq r^{n/2}$ .

Another possibility is to choose $r$ sum-free sets $A_1, \ldots, A_r$ and take all colourings of $A = A_1 \cup \cdots \cup A_r$ such that the elements of colour $i$ are contained in $A_i$ . There are

$1^{n_1} \cdot 2^{n_2} \cdots r^{n_r}$

such colourings, where $n_j$ is the number of elements in exactly $j$ of the $A_i$ . For example, we might take half of the $A_i$ to be $O$ and half to be $I$ . Then the odd numbers greater than $n/2$ are in every set, and the evens greater than $n/2$ and the odds less than $n/2$ are in half of the sets, so the number of colourings is around

$r^{n/4}(r/2)^{n/2}.$

For $r=4$ this matches the previous lower bound; for $r \geq 5$ it is larger.

It’s easy to see that this construction cannot improve the bound for $r = 2$ : it only provides $2^{n_2}$ good colourings, but $n_2 \leq n/2$ as elements contributing to $n_2$ are in $A_1 \cap A_2$ , which must be sum-free.

What about $r=3$ ? Now we get $2^{n_2}3^{n_3} = 3^{n^3 + n_2 / \log_2 3}$ good colourings. We also have that

$2n_2 + 3n_3 \leq |A_1| + |A_2| + |A_3| \leq 3n/2.$

But since $\log_2(3) > 3/2$ we have

$3^{n^3 + n_2 / \log_2 3} \leq 3^{n^3 + 2n_2 / 3} \leq 3^{n/2}.$

Moreover, if $n_2$ is not tiny then we are some distance off this upper bound, so the only good constructions in this family come from having all the $A_i$ substantially agree.

How can we get matching upper bounds? If there weren’t very many maximal sum-free sets then we could say that every good colouring arises from a construction like this, and there aren’t too many such constructions to consider. This is too optimistic, but the argument can be patched up using containers.

The container method is a relatively recent addition to the combinatorial toolset. For this problem the key fact is that there is a set $\mathcal F$ of $2^{o(n)}$ subsets of $[n]$ such that

every sum-free set is contained in some $F \in \mathcal F$ ,
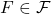each 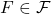$F \in \mathcal F$ is close to sum-free. Combined with a “sum-removal lemma” this means in particular that it has size not much larger than $n/2$ .

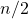We now consider running the above construction with each $A_i$ an element of $\mathcal F$ . Since the containers are not themselves sum-free, this will produce some bad colourings. But because every sum-free set is contained in some element of $\mathcal F$ , every good colouring of a subset $A$ of $[n]$ will arise in this way. And since there are most $|\mathcal F|^r$ choices for the sets $A_i$ the number of colourings we produce is at most a factor $2^{o(n)}$ greater than the biggest single example arising from the construction.

This is the big idea of the paper: it reduces counting colourings to the problem of optimising this one construction. For $r \leq 5$ the authors are able to solve this new problem, and so the original.

Leave a Reply Cancel reply